题目
分析
作为本章例题的最后一题,本题有一定的难度。但只要认真分析,还是很容易解决的。
传球分析
先要画出传球者的排位。按照题意,传递者的编号是按照逆时针排列,并首尾相连。
显然,经过每次传递,“眼镜”在哪里由两个因素决定:传球者的朝向(0|1分别代表朝内或朝外),以及传递的方向(0|1分别代表往左传或者往右传)。所以,总体的可能性有4种。假定当前位置是position,传递步数是steps:
- 向左传(
0),朝向内(0)(以下用(0, 0)这样的形式表示):position - steps (0, 1):position + steps(1, 0):position + steps(1, 1):position - steps
当然,我们需要考虑首尾相连的情况,而这是一个模运算。如果出现position-steps的处理,我们需要考虑负数求模的情况。但处理起来也很方便,我们只要计算后加一个n(总人数)的偏移在求模即可。
int position=0;
for(int i=0;i<m;i++)
{
if(orders[i].direction==0) // 向左传递
{
if(dolls[position].orientation==0) // 这个位置的小人面朝内
{
position=(position+n-orders[i].steps)%n;
}
else
{
position=(position+orders[i].steps)%n;
}
}
else // 向右传递
{
if(dolls[position].orientation==0) // 这个位置的小人面朝内
{
position=(position+orders[i].steps)%n;
}
else
{
position=(position+n-orders[i].steps)%n;
}
}
}答案
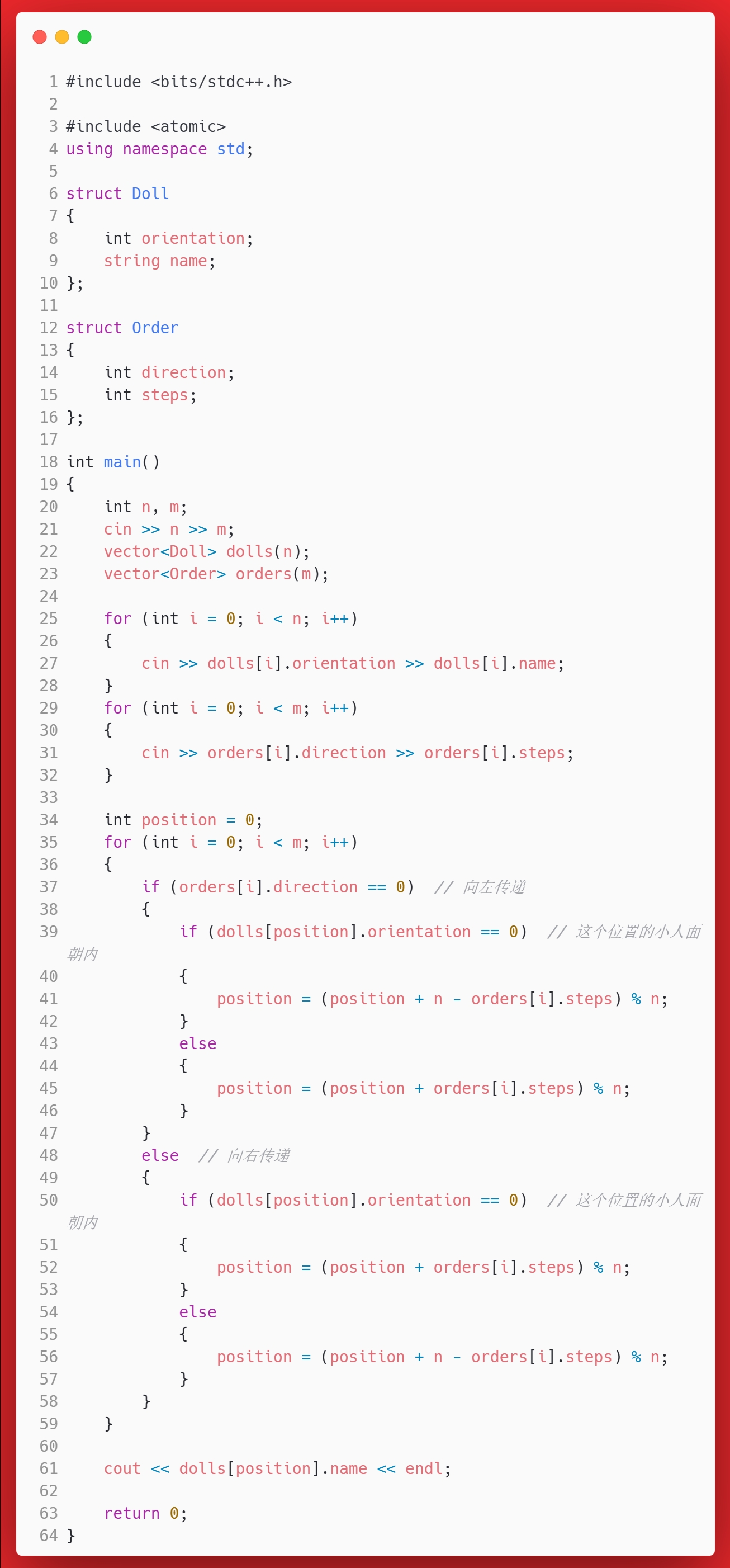
思考
这段代码略显冗长,对于四种情况,我们进行了四种处理。但仔细观察会发现,其实只有两种——简单说,就是当前位置加或者减步长。
我们总结一下:
| 情况 | 结果 |
|---|---|
| (0,0) 朝内 + 向左 | position - steps |
| (0,1) 朝内 + 向右 | position + steps |
| (1,0) 朝外 + 向左 | position + steps |
| (1,1) 朝外 + 向右 | position - steps |
显然,这里存在一个异或关系:(0, 0), (1, 1)是减,(1, 0), (0, 1)是加。于是我们可以缩短代码,并统一计算:
for (int i = 0; i < m; i++)
{
// XOR determines direction: use it to calculate +steps or -steps
int delta = (orders[i].direction ^ dolls[position].orientation) ? orders[i].steps : -orders[i].steps;
position = (position + delta + n) % n;
}
