洛谷：P1572：计算分数

题目

P1572：计算分数

分析

这道题目不难，但需要用到字符串的操作，所以做个介绍。

按照分数的加减法运算法则，分母首先要通分，然后分子交叉乘另一个分母后相加，再约简。

\(\frac{a}{b}+\frac{c}{d}=\frac{a\times d+c\times b}{bd}\)

因此必然牵涉到gcd等的运算，为了简化运算过程，可以用struct Fraction来封装，并重载+和-两个运算符，以及常规的toString()方法。再加上一些辅助函数（比如用来化简的simplify()）。

另外，由于可能出现减法，所以可以统一将负的分数变为“加一个分子为负数、分母为正数”的分数——因此，结构中-的操作符重载是可以去掉的。

另外，在运算时，可以不断判定符号、找分子/分母，然后不断相加。

// 读取分子或分母
ll readNumber(const string& expression, int& i)
{
    ll number = 0;
    while (i < expression.length() && isdigit(expression[i]))
    {
        number = number * 10 + (expression[i] - '0');
        i++;
    }
    return number;
}

答案

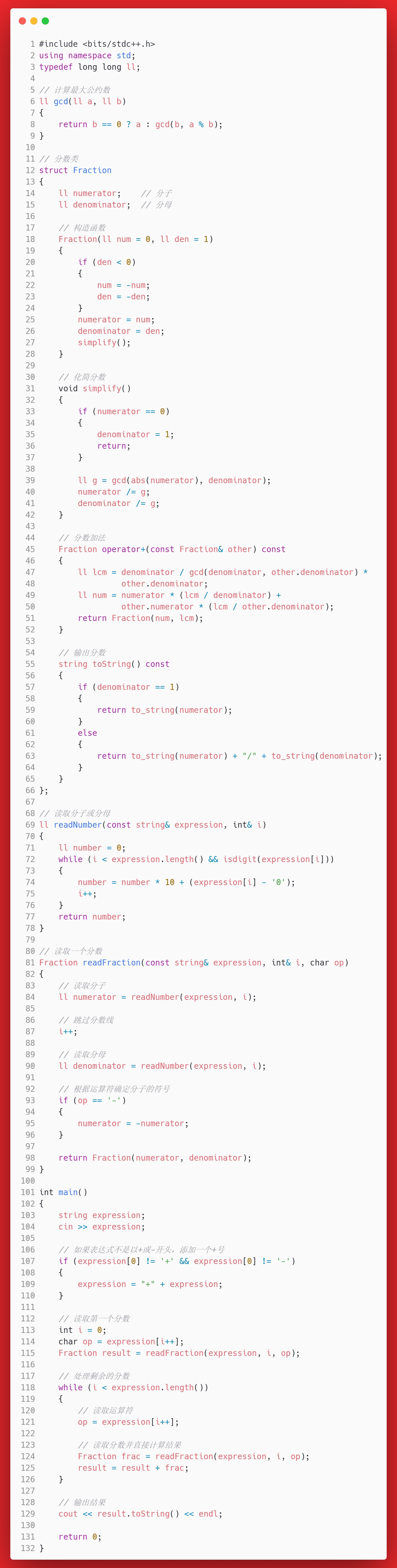
思考

（略）