题目
分析
这道题需要理解几个要点。
距离
根据题意，节点u/v之间的距离表示从u到v的最短有向路径上，向根节点的边数的两倍加上向叶节点的边数。
以样本图为例：
flowchart TD
1-->2
1-->3
2-->4
2-->5
5-->8
5-->9
3-->6
3-->7
6-->10
从节点8到6的最短距离是：8-5-2-1-3-6。其中，8-5-2-1是“向根”（的方向），走过了3条边；1-3-6是“向叶”（的方向），走过2条边。所以按照定义，距离是\(3*2+2=8\)。
LCA
根据上面的描述，我们需要找到8和6的LCA（Lowest Common Ancestor，最近公共祖先）。
8到LCA的距离，是8在树中的深度减去LCA的深度乘以2，因为这是“向根”的移动。- LCA到
6的距离，是LCA在树中的深度减去6的深度，因为这是“向叶”的移动。
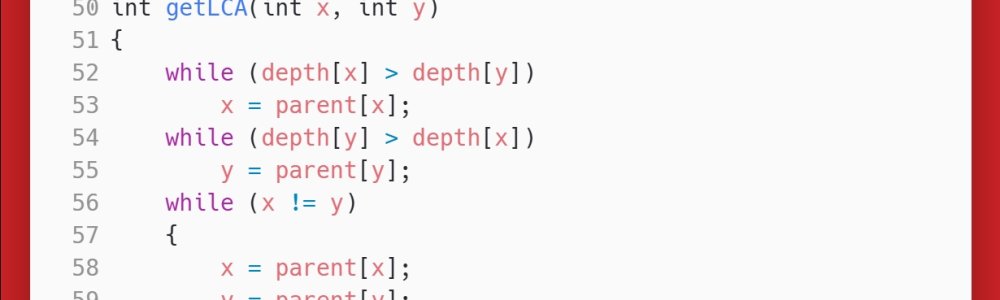
// 求LCA
int getLCA(int x, int y)
{
while (depth[x] > depth[y])
x = parent[x];
while (depth[y] > depth[x])
y = parent[y];
while (x != y)
{
x = parent[x];
y = parent[y];
}
return x;
}这个算法很有意思。它先将两个节点不断“上浮”（找到其parent），直到两者的parent深度一致。然后，再同时上浮，直到找到同一个祖先。这可以保证找到的是LCA。
节点深度和层级宽度的计算
上面的算法要求得到一个节点的深度。
直觉告诉我们，如果要得到宽度，用BFS会更好一些，因为它会首先遍历一个层级。但求深度可能用DFS更好一些。不过在本题中，我感觉宽度会更难一些，而深度简单一些。所以用BFS来求解。
在遍历每一层的时候，我们可以将当前层的深度设为之前层的深度+1。同时，更新一个levelCount数组，表示本层又“多”了一个元素。最后，遍历levelCount数组，就能找到最宽的宽度。
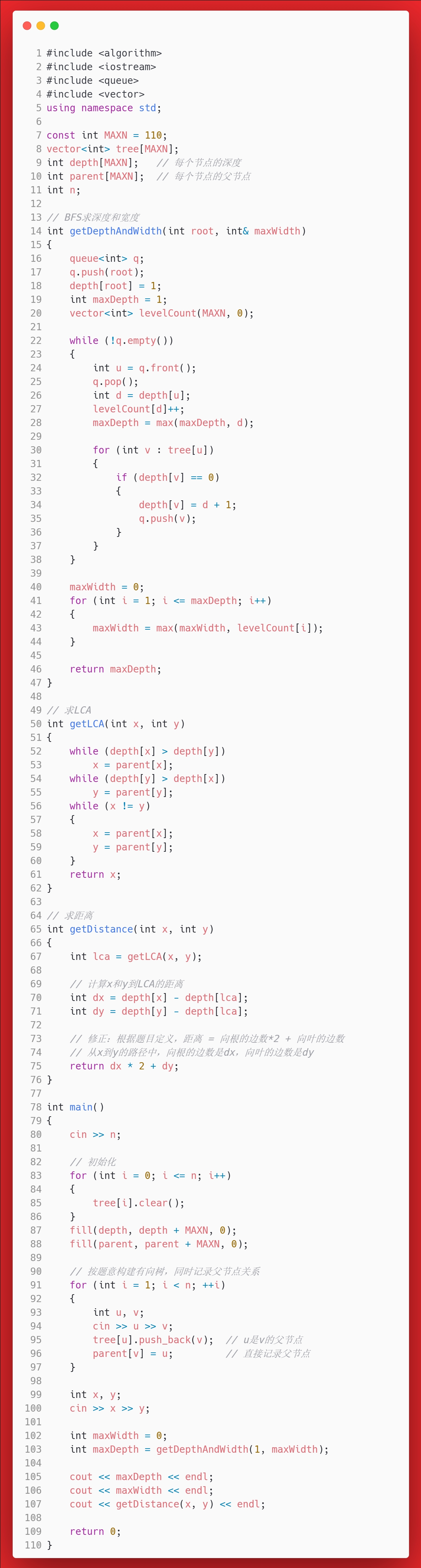
// BFS求深度和宽度
int getDepthAndWidth(int root, int& maxWidth)
{
queue<int> q;
q.push(root);
depth[root] = 1;
int maxDepth = 1;
vector<int> levelCount(MAXN, 0);
while (!q.empty())
{
int u = q.front();
q.pop();
int d = depth;
levelCount[d]++;
maxDepth = max(maxDepth, d);
for (int v : tree)
{
if (depth[v] == 0)
{
depth[v] = d + 1;
q.push(v);
}
}
}
maxWidth = 0;
for (int i = 1; i <= maxDepth; i++)
{
maxWidth = max(maxWidth, levelCount[i]);
}
return maxDepth;
}答案
思考
这里对节点间距离的定义有点新奇。