题目
分析
先说核心的算法:基于之前的经验,显然这是一个“二分”的题目。
不过这里有一个特别需要注意的点,也就是题目中明确说了的:
能量的使用是连续的……充能也是连续的……
所以,这不是一个“整数区间找整数”而是一个“区间找实数”的题目。
核心的算法(也就是“目标函数”的写法)是:
bool check(double time)
{
double charge_capacity = p * time; // 预先计算充电容量
double need = 0;
for (int i = 0; i < n; i++)
{
double consume = devices[i].consume * time;
if (consume > devices[i].energy)
{
need += (consume - devices[i].energy);
if (need > charge_capacity)
return false; // 提前返回
}
}
return true;
}注意,这里为了省时间,进行提前判定:算到第某个设备的时候,总需求的充电量超过了可以提供的充电量,就可以提前退出,不用傻傻地等到循环结束。
另外还有一个地方需要提前判定:由于充电宝的能量是无限的——它只有最大输出能量的限制——因此,如果所有设备需要的充电量小于这个最大输出能量,那么所有的设备都能永远持续运行,也就是按照题意,需要输出-1。
答案
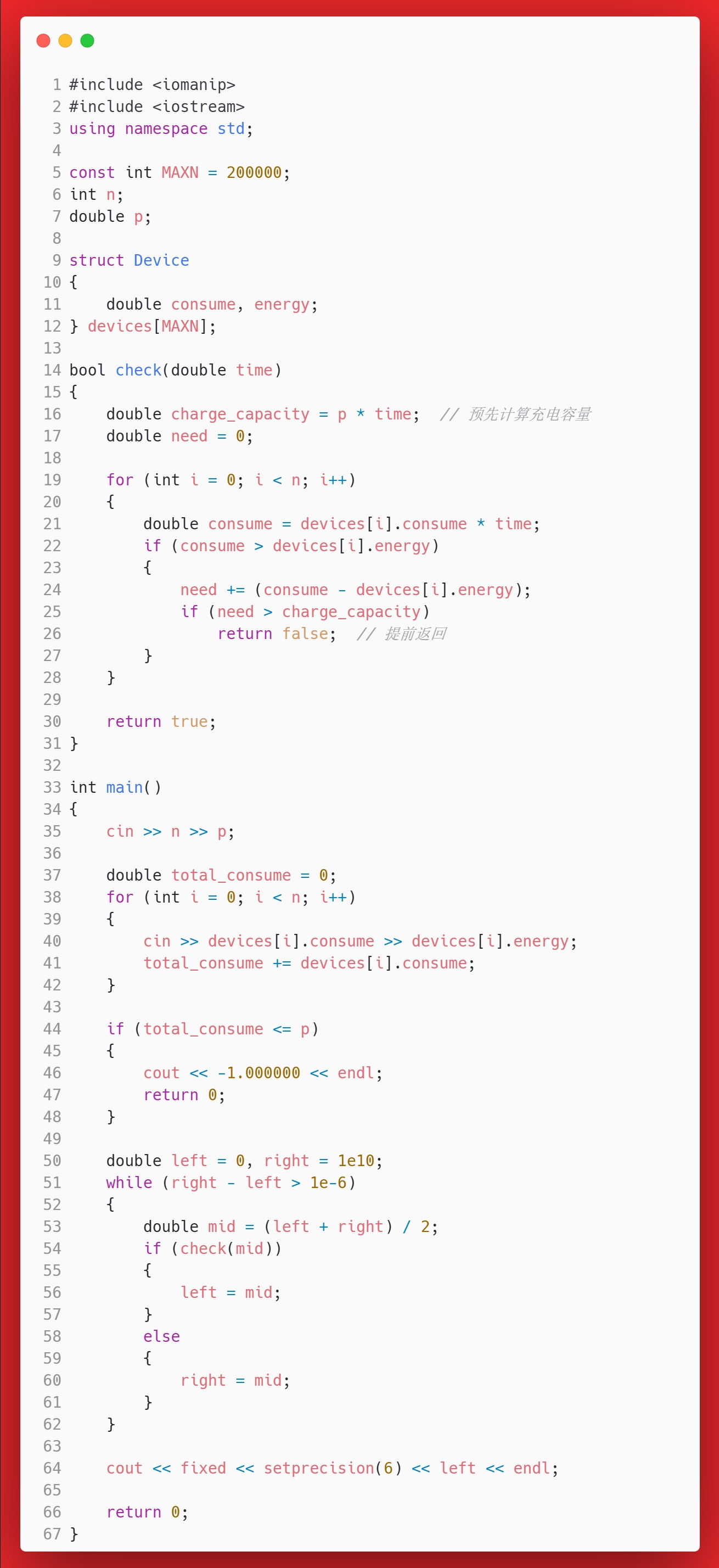
思考
这道题目不难,但我用了3次提交完成任务。
第一次,是最常规的写法。所有测试点中有一个没有通过。通过检查洛谷给出的错误信息,发现是我们的“右边界”设置的太小,于是将其从1e9调整到1e10。
第二次,同样的测试点出现了超时。于是进行了上文中提到的一些优化:提前计算总的供电量,提前退出需电量的计算等。
第三次,终于通过了。

