洛谷：P2880：Balanced Lineup

题目

P2880：Balanced Lineup

分析

这道题目的切入点是两个：ST表和分治。

我们先讨论比较简单的情况。

假定一共有8头牛，我们要求区间也包括这8头牛（也就是\([a, b]\)的长度是8）。我们当然不能用遍历的方式去找最高、最低值——因为这种做法不具有推广性。

分治的出发点

我们采用的做法是分而治之：

这样做的好处是，我们可以用递归/递推来实现。而且，对于长度为1的区间，是不用计算的——因为此时的最大值就是元素本身。

ST表的建立

将上文“分治”的思路反过来执行，就可以构造出ST表。

void build_st()
{
    // 初始化长度为1的区间
    for (int i = 1; i <= n; i++)
    {
        st_max[i][0] = h[i];
        st_min[i][0] = h[i];
    }

    // 递推计算其他区间
    for (int j = 1; (1 << j) <= n; j++)
    {
        for (int i = 1; i + (1 << j) - 1 <= n; i++)
        {
            // 区间[i, i+(2^j)-1]的最大值等于左半部分和右半部分的最大值的较大者
            st_max[i][j] =
                max(st_max[i][j - 1], st_max[i + (1 << (j - 1))][j - 1]);
            // 区间[i, i+(2^j)-1]的最小值等于左半部分和右半部分的最小值的较小者
            st_min[i][j] =
                min(st_min[i][j - 1], st_min[i + (1 << (j - 1))][j - 1]);
        }
    }
}

首先，代码初始化长度为1的区间的最值，并用st_max[i][j]表示从第i个元素开始，长度为\(2^j\)的区间的最大值。这个处理很直截了当。¹

然后，开始增加区间的长度，而且每次都是加倍（以体现\(2^k\)的特性）。此时，确定该区间st_max[i][j]的最大值就可以用递推的方式：

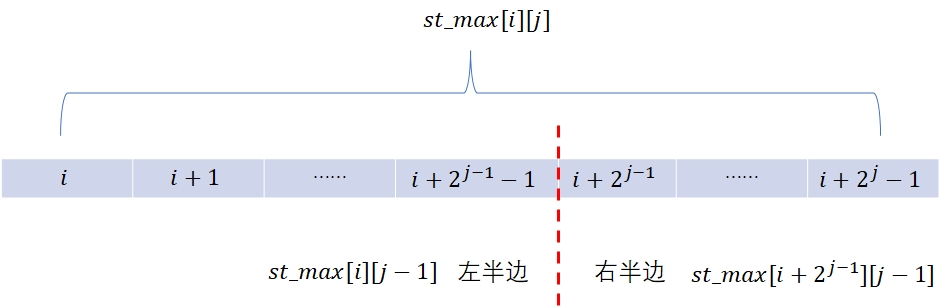
也就是代码中的：st_max[i][j] = max(st_max[i][j - 1], st_max[i + (1 << (j - 1))][j - 1]);

处理查询

对于某个查询中给出的一个区间\([l, r]\)，我们应该将其分成符合ST表分割的两个部分（可以重叠）。方法是：

int k = log2(r - l + 1);
return max(st_max[l][k], st_max[r - (1 << k) + 1][k]);

我们先求出这个区间的长度（\(r-l+1\)），然后得到使得\(2^k\le (r-l+1)\)最大的那个\(k\)。然后将原来的区间分为两部分：\(st\_max[l][k], st\_max[r - (1 << k) + 1][k]\)。

综合上述算法，就可以得到最终的代码。

答案

思考

有关“ST表”以及一些相关概念的讨论，这里有一篇很好的文章可以参考。

另外，可以思考一下：为什么st_max[l][k], st_max[r - (1 << k) + 1][k]这两个区间一定会全覆盖原来的区间。