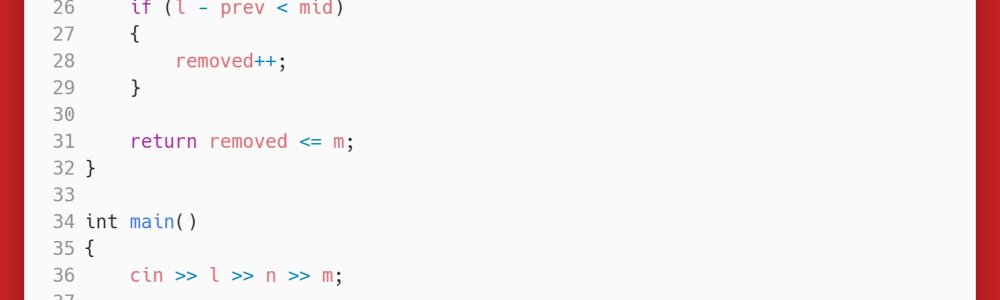洛谷：P2678：跳石头

题目

P2678：跳石头

分析

这道题目和OJ上的题目“河中跳房子”是一样的。都是“贪心”加上“二分”的。但这题中，二分反而更重要，所以洛谷将其归类在“二分”类。

参考“进击的奶牛”中的思路：

我们不知道合理的d是多少，但直觉告诉我们d总有个上限——超过这个上限后就肯定放不下了。所以很适合用二分法。

其他代码其实都差不多。

答案

思考

虽说这道题目和OJ上的题目“河中跳房子”是一样的，但古怪之处在于，我用OJ上通过的代码试着提交的时候，有一个测试用例不能通过。经过和AI的讨论，发现OJ的测试用例比较宽松，所以就过了，而洛谷的测试用例考虑到了一个极端的边界条件，所以就没有通过。

主要问题出在二分时左右边界的调整上。

    // OJ可通过的代码
    while(s+1<e)
    {
        mid=(s+e)/2;
        if(valid(mid))
        {
            s=mid;
            result=mid;
        }
        else{
            e=mid;
        }
    }

而两边都能通过的代码是：

    // 二分查找最大的可能跳跃距离
    while (left <= right)
    {
        int mid = left + (right - left) / 2;
        if (valid(mid))
        {
            ans = mid;
            left = mid + 1;  // 尝试更大的距离
        }
        else
        {
            right = mid - 1;  // 尝试更小的距离
        }
    }

原始OJ代码的问题，是保留终点mid作为答案。由于我们的二分循环条件是s+1<e，所以总有一个当中的中值：比如s=3而e=5时就终止了，但此时有个mid=4。这么做的问题在于，5也可能是可行的——于是就给出了错误答案。

所以，正确的代码采用了更保守的做法，保证永远能达到边界。