题目
分析
这是一道经典的二维数组模拟入门题目。
我们先看一般形式:
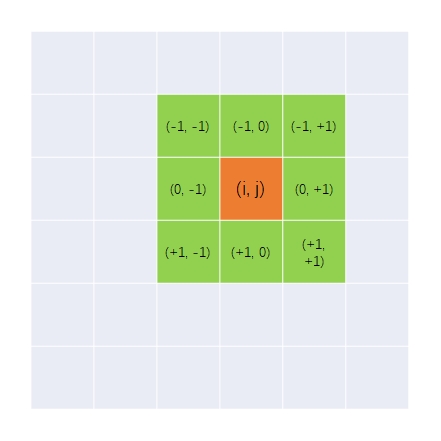
对于位于(i, j)的格子来说,有两种情况:
- 这里是个地雷:
board[i][j]=='*',那么原样输出。 - 这里不是地雷。那么需要检查它周边共8个格子的情况,统计总共有几颗地雷并输出该数量。
如何检查周边的8个格子?从上图可以看出,对于位于(i, j)的格子来说,其周边8个邻居格子的坐标完全是由(i, j)确定的。这是一个常见的需求,这里给出一个比较通用的方法:设置一个有8个元素、代表8个方向的数组。
struct Direction
{
int x;
int y;
};
Direction dir[8] = {{-1, 0}, {-1, 1}, {0, 1}, {1, 1},
{1, 0}, {1, -1}, {0, -1}, {-1, -1}};这样,我们在走到某个格子的时候,就可以简单地用循环遍历这8个方向的格子,方法是对(i, j)分别加上对应的偏移量。
// ...
for (int k = 0; k < 8; k++)
{
int x = i + dir[k].x;
int y = j + dir[k].y;
if (board[x][y] == '*')
{
count++;
}
}
// ...边界检查
需要注意的是,如果(i, j)来到了棋盘的边界,那么对坐标进行\(\pm 1\)的操作就会引起越界。我们可以在上面代码的循环中进行判定(比如加上if (x<0)),但这会引起代码臃肿。
比较常用的方法是在实际的棋盘四周各加上一圈“虚拟”格子并且初始化为空或者任何非'*'的字符。
const int MAX = 105;
char board[MAX][MAX];实际中,通常把真实棋盘放在 board[1..n][1..m],并通过将board设置为全局变量而初始化为非雷字符,以保证访问虚拟边界时不会误判。
题目中,明确说明棋盘尺寸不会超过100,我们将尺寸设置为105,就能完全地包括棋盘周围虚拟出来的一圈边界。这样一来,所有的“边界”判定就不存在了,因为我们可以确保的是,从(1, 1)到(n, m)的所有格子在进行周围格子遍历的时候,都不可能越界,最坏的情况就是访问到虚拟的格子!
答案

思考
(略)

