题目
分析
前缀和
看到要不断地求一个区间的和，是使用“前缀和”的强烈提示。只要求出前缀和，就可以在\(O(1)\)的时间里求出任意区间\([l, r]\)的和：\(prefix\_sum[r]-prefix\_sum[l-1]\)。
for (int i = 1; i <= n; i++)
{
cin >> a[i];
prefix_sum[i] = prefix_sum[i - 1] + a[i];
}单调队列
同时，求区间极值的问题，也是使用“单调队列”的强烈提示。它的基本算法如下：
flowchart TD
A["元素索引i从1到n的循环"]-->
B{"只要q不空，且i-q.front()>m（超出长度）"}-->
|Y|C["弹出q.front()"]-->B
B-->|N|D{"只要q不空"}-->
|Y|E["用前缀和计算区间和：区间起点q.front, 终点i"]-->E
D-->|N|F["维持单调队列"]-->
G["当前索引入队列"]
结合流程图进一步说明如下：
while (!q.empty() && i - q.front() > m)
{
q.pop_front();
}这段代码是为了保证单调队列中所有的“位置”都是和当前考虑的位置i在大小为m的区间里。如果i=q.front()>=m就说明q.front()所在的位置已经超出了，不用再考虑。
if (!q.empty())
{
max_sum = max(max_sum, prefix_sum[i] - prefix_sum[q.front()]);
}这段代码是计算以当前位置结尾的最大子段和。注意，这里只减了一次，而m是个区间。为什么不需要循环处理呢？我们继续看代码。
//第三段代码
while (!q.empty() && prefix_sum[q.back()] >= prefix_sum[i])
{
q.pop_back();
}这段代码维护单调队列，保证队列中的元素对应的前缀和是单调递增的。
我们回头来讨论m虽然定义了一个区间，但我们不用循环处理的问题。
考虑两种情况。
第一种情况，元素都是正数，因此前缀和都是递增的。例如：
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 元素 | - | 1 | 2 | 4 |
| 前缀和 | 0 | 1 | 3 | 7 |
这种情况下，要想获得一个更大的区间和，在右边界确定（i）的前提下，左边界越小越好。也就是说，这样才能加上更多的正数，所以和会更大。
第二种情况，元素是正负交错的，因此前缀和不再严格递增。例如：
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 元素 | - | 1 | -2 | 4 |
| 前缀和 | 0 | 1 | -1 | 3 |
这种情况下，要想获得一个更大的区间和，在右边界确定（i）的前提下，左边界越大越好。也就是说，这样才能避免加上负数，所以和会更大。
体现在代码上就是上面的第三段代码。
答案
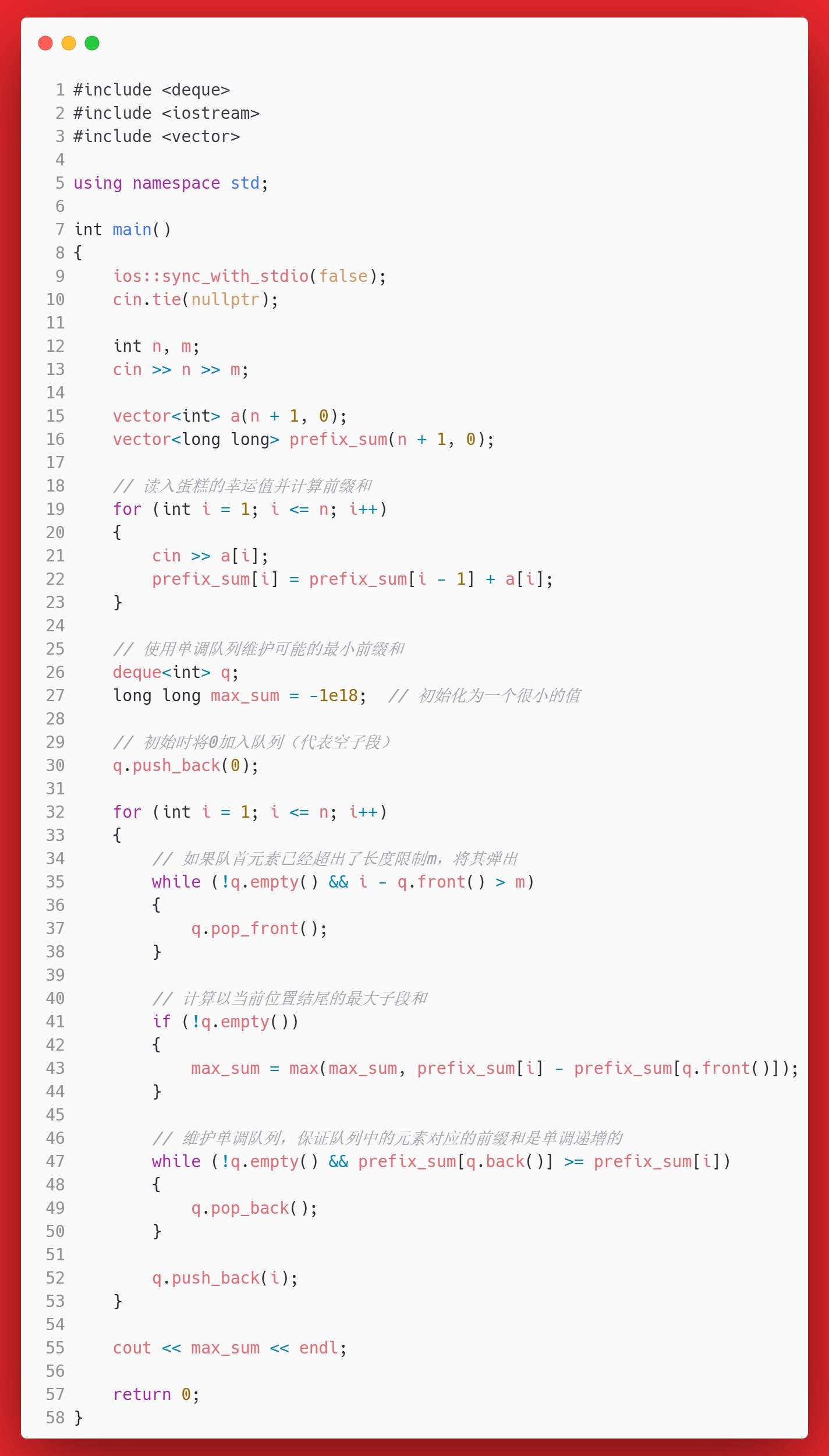
思考
本题的关键有两个：前缀和以及（前缀和）的单调递增队列，从而保证了只要用队首下标进行计算，不用考虑m所蕴含的区间，提升了效率，整个算法复杂度降低为\(O(n)\)。