题目
分析
本题着重于高精度计算中的加法运算,而这是一个模拟过程。
回想我们进行加法时的列竖式过程,从中可以直观地转换到算法。
高精度类
本题解法中,我用到了C++的类。这是高级语法,不要求掌握。不过其中讨论的基本思路是适用的,稍加改造就可以变成纯数组实现。
先给出类的定义如下:
class HighPrecision
{
friend istream& operator>>(istream& is, HighPrecision& hp);
friend ostream& operator<<(ostream& os, const HighPrecision& hp);
friend HighPrecision operator+(const HighPrecision& hp1,
const HighPrecision& hp2);
private:
vector<int> num;
public:
HighPrecision() {}
HighPrecision(const string& s)
{
for (int i = s.size() - 1; i >= 0; i--)
num.push_back(s[i] - '0');
}
};首先,我们重载两个运算符(输入和输出)。这个内容不要求掌握。
然后重载+运算,然后是用来存放各位数字的一个私有成员vector<int> num,并声明两个构造函数。请注意第二个构造函数HighPrecision(const string& s)的实现:它是把数字的位从低位到高位依次存放(也就是将字符串的末尾字符先放入 num[0])。之所以这样存放,是为了后续加法时可以从低位开始顺序遍历各个位数,便于处理进位。
实现加法
回顾列竖式加法的过程:各位对齐,从最低位开始两两相加得到一个和。这个和如果大于等于10,那么就会产生进位。我们需要将进位记下来,而当前位只保留这个和的个位数。后续各位相加的时候,要算上“进位”的数值。
用代码实现的时候,我们可以直接将“进位”先加到下一位,这样就不用专门处理进位加法。也就是说,不用a + b + carry,而是直接这么做:
hp.num[i] += a + b;
hp.num[i + 1] = hp.num[i] / 10; // Carry to next position
hp.num[i] %= 10; // Keep only the digit这样一来,在算下一位的时候,结果的hp.num[i+1]位已经有了进位,可以直接加a + b了。
结果的位数
输入的两个数字的位数不一定相同,而且相加后可能会多出一位(也就是进位的那一位)。不过,我们用的是vector,它的大小是动态调整的,不用刻意预留。如果你用静态数组保存最终结果,就需要考虑这个问题,要将数组的大小设为int result[max_digit+1],其中的max_digit是两个加数中更长的位数。
去掉前导0
题目中没有说输入就一定是规范的,所以可能出现0000000000001 + 0000034454这样的情况,也就是结果数组中有大量的前导0。但我们的输出必须规范。所以要去掉这些前导0(但如果只有一个0,这个0必须保留)。
// Remove leading zero if no final carry
if (hp.num.back() == 0 && hp.num.size() > 1)
{
hp.num.pop_back();
}答案
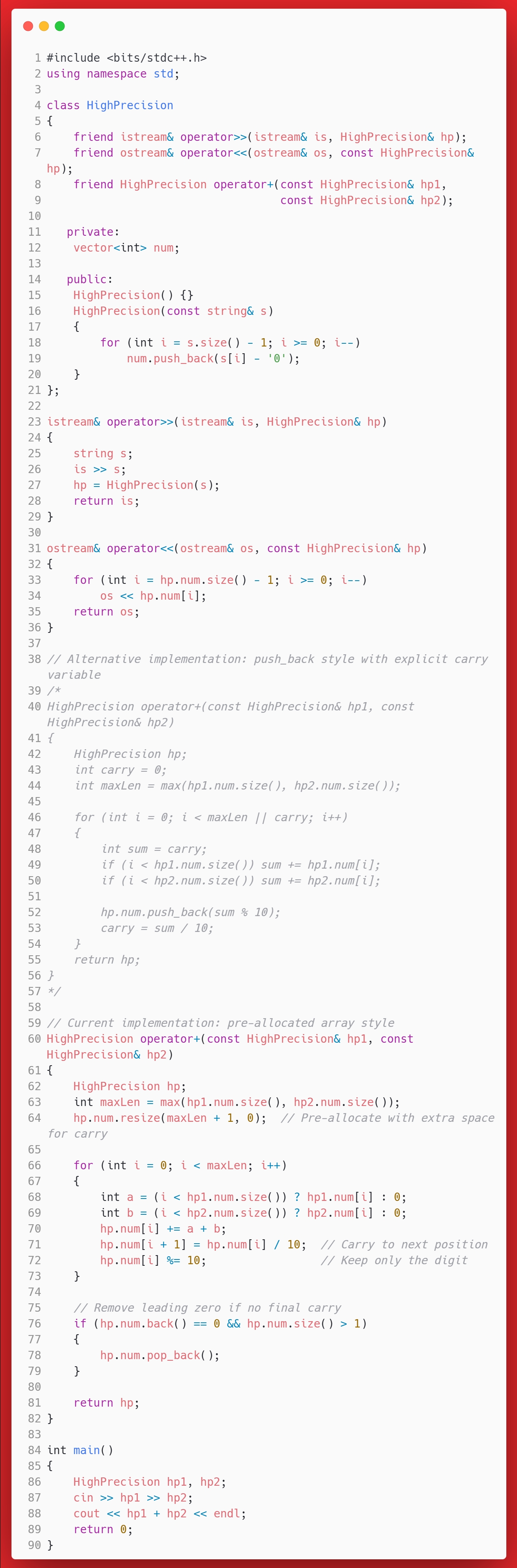
思考
加法的算法还可以更简单一些:
HighPrecision operator+(const HighPrecision& hp1, const HighPrecision& hp2)
{
HighPrecision hp;
int carry = 0;
int maxLen = max(hp1.num.size(), hp2.num.size());
// 循环条件:当仍有未处理的位或仍有进位时继续
for (int i = 0; i < maxLen || carry; i++)
{
int sum = carry;
if (i < hp1.num.size()) sum += hp1.num[i];
if (i < hp2.num.size()) sum += hp2.num[i];
hp.num.push_back(sum % 10);
carry = sum / 10;
}
return hp;
}这两种写法是等价的。

