洛谷：P1414：又是毕业季II

题目

P1414：又是毕业季II

分析

这题不太难，但要想清楚解题思路。如果我们按照题意，分别选1/2/.../k个数，就牵涉到排列组合以及多次求多个数字的gcd问题。

我们可以这样来做：

1. 对于每一个数字，列出它所有的因子。用一个数组来保存不同的因子的数量。这n个数都做好这个处理后，我们就应该有一个cnt[i]数组，表示因子i在n个数中出现了几次。
2. 由于我们要找最大的公约数，所以我们先倒序遍历所有的因子¹。某个因子i一定出现了cnt[i]次，所以它就是选择1到cnt[i]个数时，最大的那个公约数。

答案

思考

请注意代码中的24-38行，这样的代码出现过很多次。可以作为一个标准模板牢记。

    // 统计每个因子能被多少个学生的能力值整除
    for (int i = 1; i <= n; i++)
    {
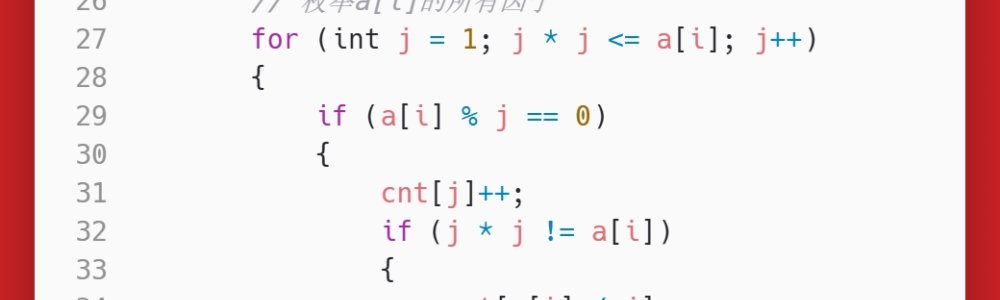
        // 枚举a[i]的所有因子
        for (int j = 1; j * j <= a[i]; j++)
        {
            if (a[i] % j == 0)
            {
                cnt[j]++;
                if (j * j != a[i])
                {
                    cnt[a[i] / j]++;
                }
            }
        }
    }