题目
分析
高精度
首先,这道题目需要用到高精度乘法,但在本文中不展开说明,请参考A*B Problem。
核心算法
先分析一个样本数据:如果数字的和是10,那么怎么拆分呢?
一开始的一个误区可能是:算术平均大于几何平均:\(\frac{a+b}{2}\ge\sqrt {a\times b}\),而等号成立当且仅当\(a==b\)时。但是测了一下,发现不是这么简单。比如10=5+5,进一步变化为4+6,此时\(4\times 6=24\),但这不是最大的——最大的乘积出现在\(2\times 3\times 5\)。又试了几个,发现了另一个算法。
从2开始,依次加3,加4……但保证最后还是\(2+3+4+...+k\lt n\),到最后,一定存在一个差值\(diff=sum+(k+1)-n\)。根据这个\(diff\),有几种处理方式:
diff==0,那么k+1可以直接加入。diff==1,那么去掉2,最后一个k变成k+1即可。diff>=2,直接去掉某个等于diff的数即可。
核心算法如下:
累加过程
vector<int> result;
// 从2开始选择连续的自然数
int current = 2;
int sum = 0;
while (sum + current < n)
{
result.push_back(current);
sum += current;
current++;
}调整过程
// 计算超出的部分
int diff = sum + current - n;
if (diff == 0)
{
// 刚好等于n,加入最后一个数
result.push_back(current);
}
else if (diff == 1)
{
// 超出1,去掉2,将最后一个数加1
for (int i = 0; i < result.size(); i++)
{
if (result[i] == 2)
{
result.erase(result.begin() + i);
break;
}
}
result.push_back(current + 1);
}
else
{
// 超出diff,去掉等于diff的数,加入current
// 根据数学证明,diff必定在[2,3,...,k]中,所以一定能找到
for (int i = 0; i < result.size(); i++)
{
if (result[i] == diff)
{
result.erase(result.begin() + i);
break;
}
}
result.push_back(current);
}这个算法的基础在于,对于比较大的n,\((n/2)!\)一定比\(\frac{n}{2}\times \frac{n}{2}=\frac{n^2}{4}\)大。
答案
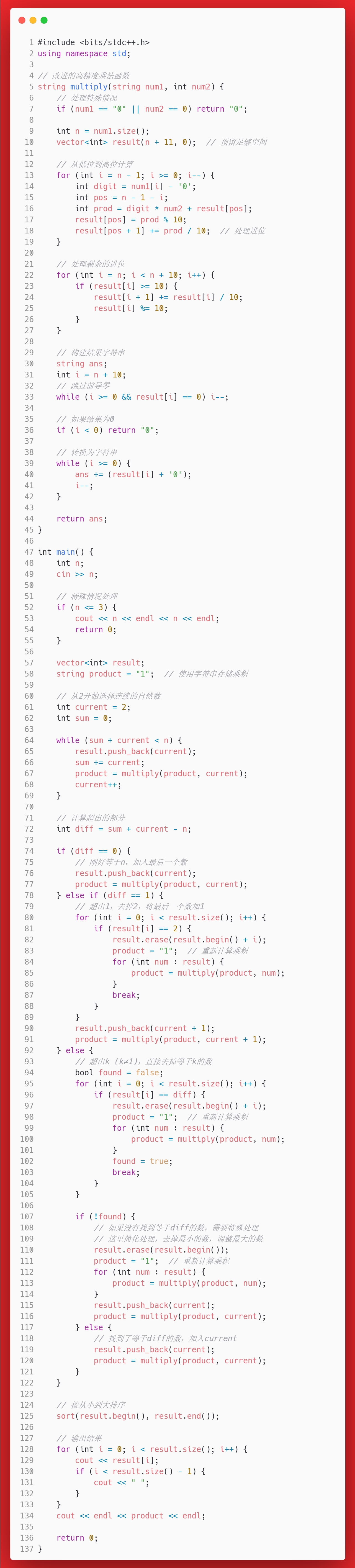
思考
(略)

