洛谷：P1177：排序（模版）

题目

P1177：排序（模版）

分析

题目说了，这是一个“模版”，用来帮助我们理解分治的基本思想和基本应用（归并排序）。

基本的分治思想

很简单，分治就是“分而治之”。以排序为例，如果数组里有很多数据，之前的初级排序都会很耗时（例如：冒泡排序就是典型的时间复杂度在\(O(N^2)\)的算法）。怎么加快呢？冒泡排序之所以慢，是因为一个数值到达最终位置的时候，要多次与相邻数值比较。直觉告诉我们：如果比较次数少了，速度自然就快了。降低比较次数，从降低要比较的数量开始。

将整个数据集分成左右两半：\([L, R] \Rightarrow [L, m], [m+1, R]\)，其中\(m=\frac{L+R}{2}\)。对于这两个小区间，又可以各自两分……直到区间只有一个数，就是自然排好序的。这种两分思路可以缩短总的比较次数，但还有一个问题没有解决：两个区间有序了，但如何整合到一个更大的区间使其有序？

归并思路

观察如下两个区间各自排序后的数据：

A: [1 4 | 2 5]

显然，最后排好序的数组应该是1 2 4 5。

这里可以用双指针法分别指示左右区间下一个要看的数字的位置（分别是i和j），同时用一个临时数组tmp[]来存放：

1. \(\texttt{A[i]}\le \texttt{A[j]}\)，说明A[i]在前，拿出A[i]给tmp[k]——这里的k指示tmp数组中下一个要处理的位置。A数组左边部分要看下一个（i++）。tmp数组的定位也要前进一次（k++）。
2. \(\texttt{A[i]} > \texttt{A[j]}\)，说明A[j]在前，拿出A[j]给tmp[k]——这里的k指示tmp数组中下一个要处理的位置。A数组右边部分要看下一个（j++）。tmp数组的定位也要前进一次（k++）。
3. 上述循环一直进行到i>mid||j>r为止：while(i<=mid && j<=r)
4. 上述循环结束后，要么左边区间、要么右边区间还有数据留存，所以要将这些数据转移到tmp中。

    while(i<=mid)
    {
        tmp[k++]=a[i++];
    }
    while(j<=r)
    {
        tmp[k++]=a[j++];
    }
    for(int i=0;i<k;i++)
    {
        a[l+i]=tmp[i];
    }

5. 将tmp数组拷贝回A数组，以便进行下一次合并。

这就是归并排序的核心思路。

答案

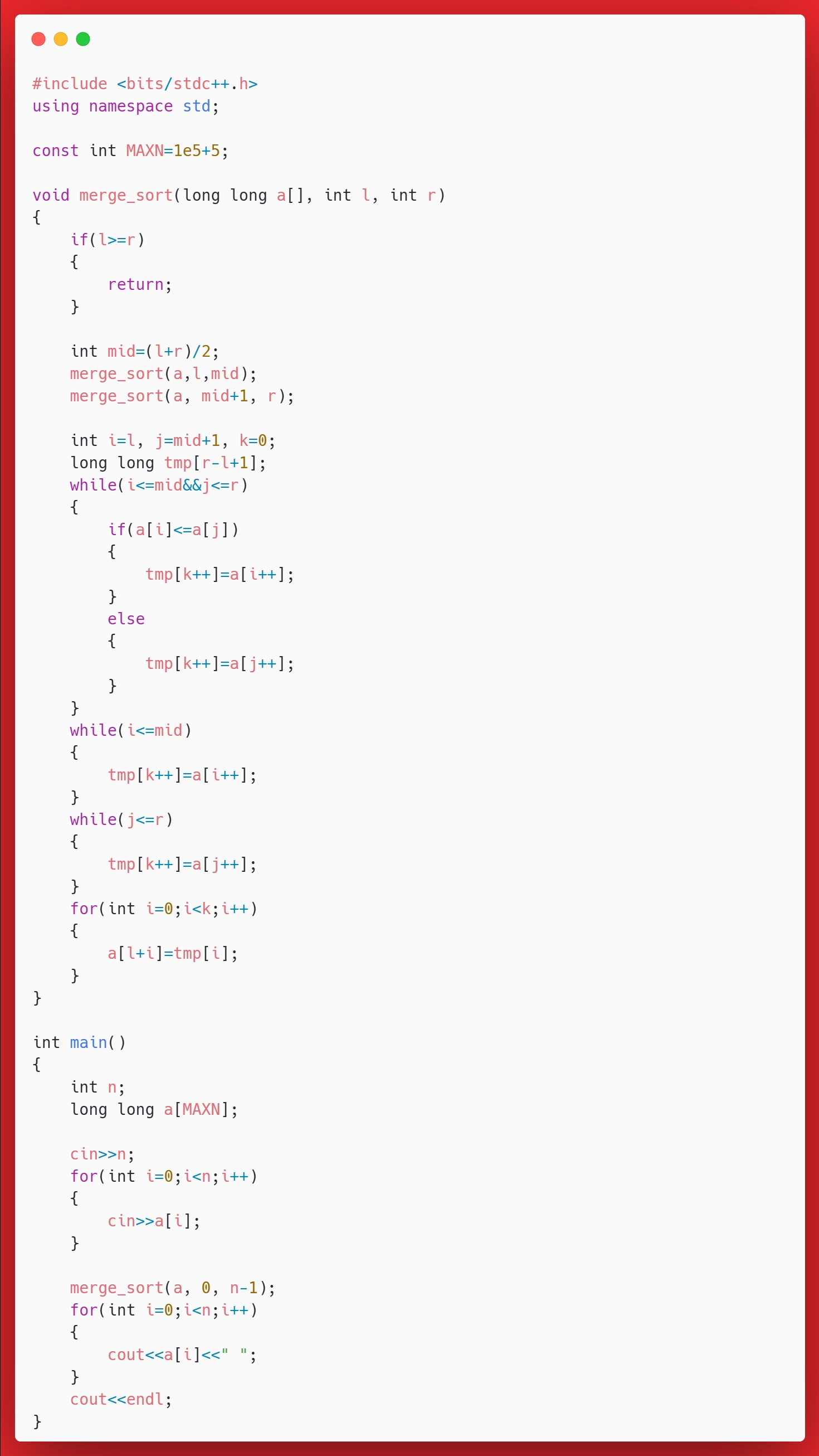
思考

请牢记这个模板。

251217更新记录：

重新看第9章，发现这题其实是快速排序的模版题，因此重做了一次。先将代码贴出：

简单说一下算法思路：

1. 找到一个“哨兵”。本解法是用当前区间的中间作为“哨兵”：int pivot = numbers[(l + r) / 2];
2. 先保留左右区间的原始值：int left = l, right = r;
3. 双指针法：
   1. 如果numbers[left] < pivot，那么这个数字留在“左边”是对的，所以找下一个：left++。
   2. 如果numbers[right] > pivot，那么这个数字留在“右边”是对的，所以找前一个：right--。
4. 我们总会来到一个点，此时numbers[left] >= pivot && numbers[right] <= pivot。
5. 这两个数字形成了所谓的“逆序对”，需要交换。（当然，我们要检查一下此时left <= right）。
6. 只要left <= right，我们就要继续进行这样的逆序对检查。直到两个指针出现了交叉：left > right。
7. 通过以上步骤，我们将比哨兵大的数值集中到了右边，比哨兵小的数值集中到了左边。
8. 对左右两边继续递归排序，但要注意：
   1. 此时的左边区间范围：[l, right]。
   2. 此时的右边区间范围：[left, r]。